Tupel wie Gruppe/Körper/Polynom

(G, *) Gruppe

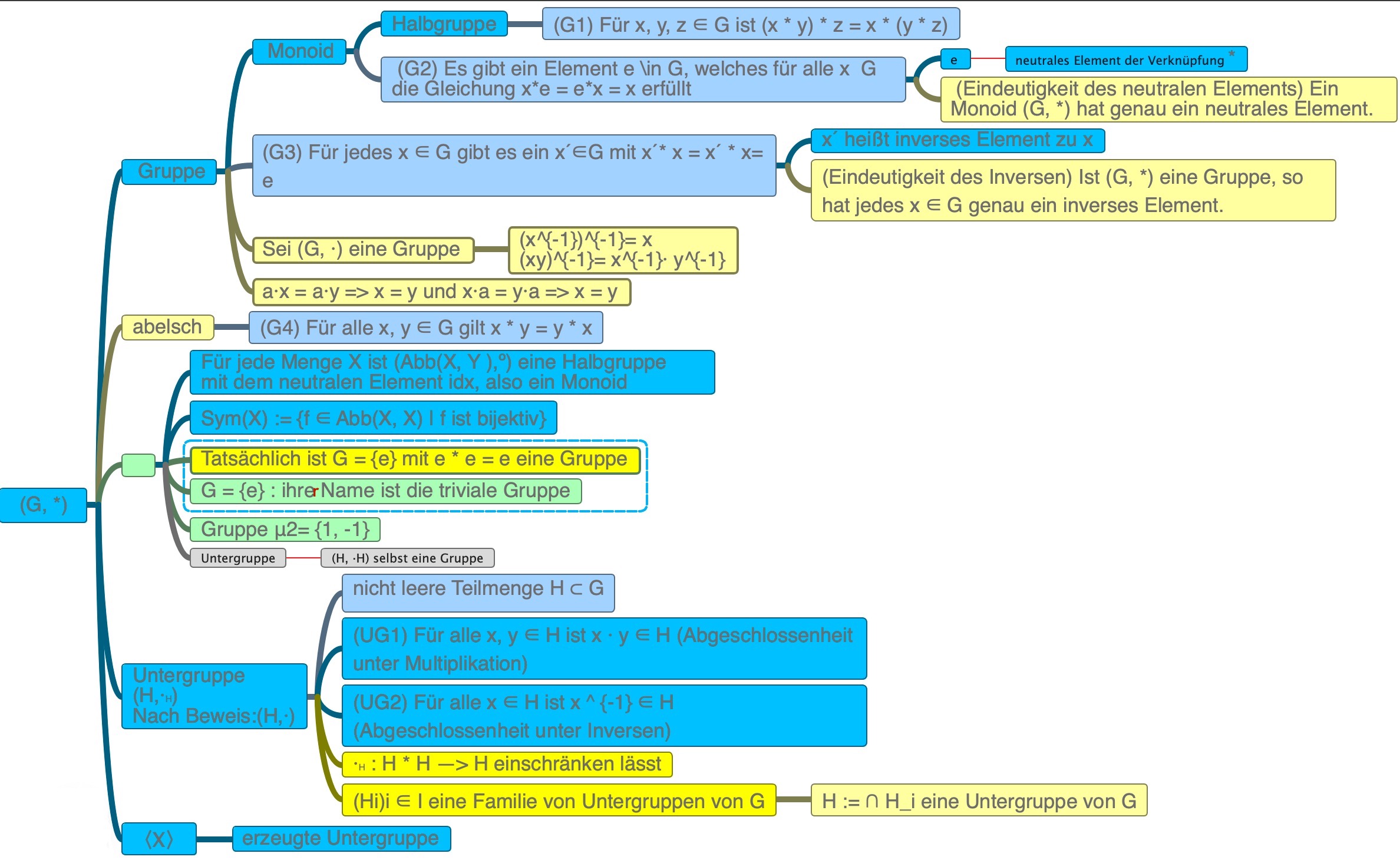(G, *) als Halbgruppe (G1 erfüllt)

(G1) Für x, y, z ∈ G ist (x * y) * z = x * (y * z)

Monoid (G1 und G2 erfüllt)

(G2) Es gibt ein Element e \in G, welches für alle x G die Gleichung xe = ex = x erfüllt

e neutrales Element von G

(Eindeutigkeit des neutralen Elements) Ein Monoid (G, *) hat genau ein neutrales Element.

Gruppe (G1, G2 und G3 erfüllt)

(G3) Für jedes $x ∈ G$ gibt es ein $x´∈ G$ mit $x´ * x = x´ * x= e$

$x´$ heißt inverses Element zu $x$

(Eindeutigkeit des Inversen) Ist (G, *) eine Gruppe, so hat jedes x ∈ G genau ein inverses Element.

(Satz 2) (xy)^{-1}= x^{-1}· y^

(satz3) a·x = a·y => x = y und x·a = y·a => x = y

abelsche Gruppe

(G4) Für alle x, y ∈ G gilt x * y = y * x

---

Beispiele der Gruppe

• Für jede Menge X ist $(Abb(X, Y ),º)$ eine Halbgruppe mit dem neutralen Element idx, also ein Monoid

• $Sym(X) := \{ f ∈ Abb(X, X) |\text{ f ist bijektiv} \}$

• Tatsächlich ist G = {e} mit e * e = e eine Gruppe

G = {e} : ihrer Name ist die triviale Gruppe

• $μ2= \{1, -1 \}$ Gruppe

• Untergruppe $(H, ·_H)$ ist selbst eine Gruppe

---

Untergruppe

Nach Beweis:(H,·)

nicht leere Teilmenge H ⊂ G

(UG1) Für alle x, y ∈ H ist x · y ∈ H (Abgeschlossenheit unter Multiplikation)

(UG2) Für alle x ∈ H ist x＾{-1} ∈ H (Abgeschlossenheit unter Inversen)

$·_H : H * H \to H$ einschränken lässt

$(H_i)_i \in I$ eine Familie von Untergruppen von G

$H := ∩ H_i$ eine Untergruppe von G

〈X〉

erzeugte Untergruppe

Ring und Körper

Polynom

K-Vektorraum

Lineare Kombinarion