Menge

##$\text{Menge }A$

Definition: ________(später)

Direkt Verstehen

• Die Zusammenhang der mathematischen Angelegenheiten

  • die Mathematische Angelegenheiten in einer Menge heißt Elemente der Mengen

• Existierendes Problem: Das Russellsche Paradoxon$ M ∶= {x ∣ x \notin x }$

Definition der ZKM

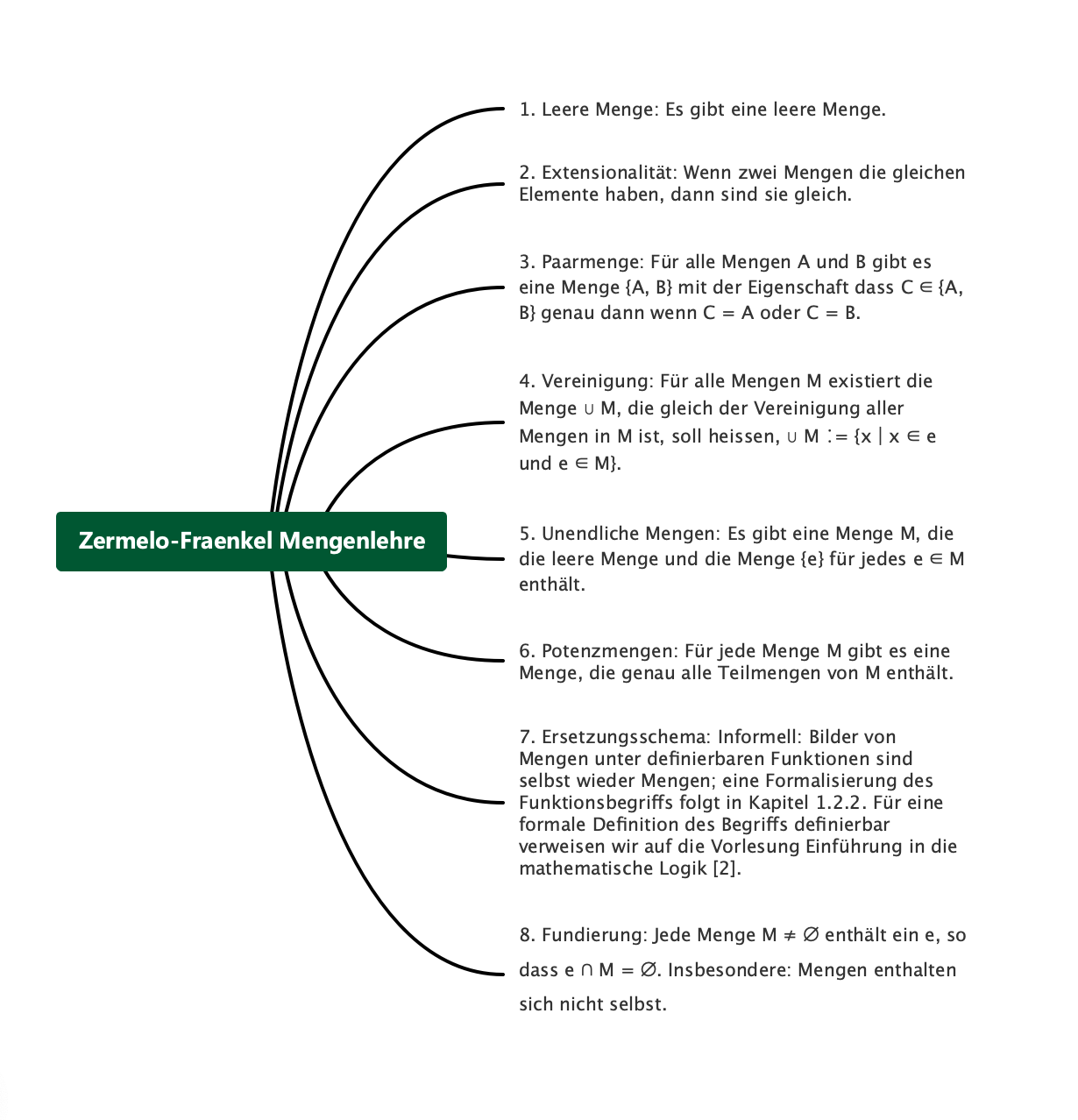
1. Leere Menge: Es gibt eine leere Menge.

2. Extensionalität: Wenn zwei Mengen die gleichen Elemente haben, dann sind sie gleich.

3. Paarmenge: Für alle Mengen A und B gibt es eine Menge {A, B} mit der Eigenschaft dass C ∈ {A, B} genau dann wenn C = A oder C = B.

4. Vereinigung: Für alle Mengen M existiert die Menge ⋃ M, die gleich der Vereinigung aller Mengen in M ist, soll heissen, ⋃ M ∶= {x ∣ x ∈ e und e ∈ M}.

5. Unendliche Mengen: Es gibt eine Menge M, die die leere Menge und die Menge {e} für jedes e ∈ M enthält.

6. Potenzmengen: Für jede Menge M gibt es eine Menge, die genau alle Teilmengen von M enthält.

7. Ersetzungsschema: Informell: Bilder von Mengen unter definierbaren Funktionen sind selbst wieder Mengen; eine Formalisierung des Funktionsbegriffs folgt in Kapitel 1.2.2. Für eine formale Definition des Begriffs definierbar verweisen wir auf die Vorlesung Einführung in die mathematische Logik [2].

8. Fundierung: Jede Menge M ≠ ∅ enthält ein e, so dass e ∩ M = ∅. Insbesondere: Mengen enthalten sich nicht selbst.

1. Leere Menge: Es gibt eine leere Menge.

2. Extensionalität: Wenn zwei Mengen die gleichen Elemente haben, dann sind sie gleich.

3. Paarmenge: Für alle Mengen A und B gibt es eine Menge {A, B} mit der Eigenschaft dass C ∈ {A, B} genau dann wenn C = A oder C = B.

4. Vereinigung: Für alle Mengen M existiert die Menge ⋃ M, die gleich der Vereinigung aller Mengen in M ist, soll heissen, ⋃ M ∶= {x ∣ x ∈ e und e ∈ M}.

5. Unendliche Mengen: Es gibt eine Menge M, die die leere Menge und die Menge {e} für jedes e ∈ M enthält.

6. Potenzmengen: Für jede Menge M gibt es eine Menge, die genau alle Teilmengen von M enthält.

7. Ersetzungsschema: Informell: Bilder von Mengen unter definierbaren Funktionen sind selbst wieder Mengen; eine Formalisierung des Funktionsbegriffs folgt in Kapitel 1.2.2. Für eine formale Definition des Begriffs definierbar verweisen wir auf die Vorlesung Einführung in die mathematische Logik [2].

8. Fundierung: Jede Menge M ≠ ∅ enthält ein e, so dass e ∩ M = ∅. Insbesondere: Mengen enthalten sich nicht selbst.